In June, there was only one day here in Salem that was below normal -- June 1st, at -0.5°F below average. For the month we were 7.5°F above average, with only 0.67 inches of rain, just 45% of average. Ugly.
Is this high, prolonged heat wave due to manmade global warming? Would this heat wave have happened in a world without AGW? I don't know. Cliff Mass says it's just natural variability, but others have disagreed with him in the past.
But here's something: a warmer world increases the chances of extreme temperatures exponentially.
Here's what I mean, with some gory details, but not too bad. And I get to practice my LaTeX, which I wrote my thesis in but haven't used since.
 Suppose the background temperature of the world is T1, and we want to calculate the probability of an event with temperature T -- that is, the change of occurence of temperature T.
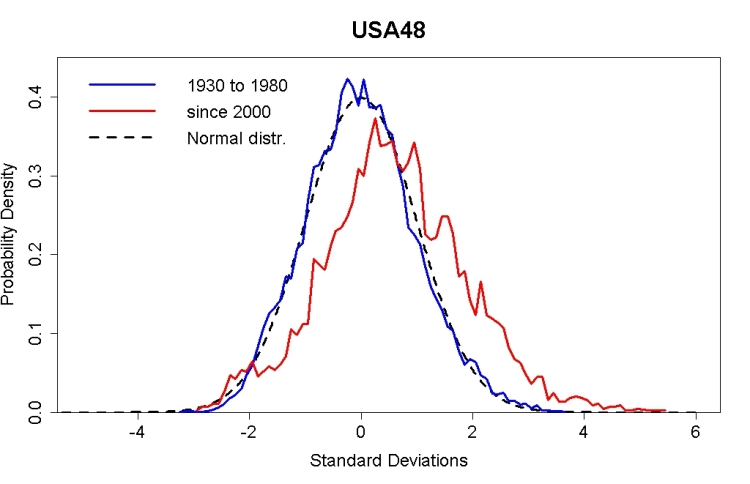
Suppose the background temperature of the world is T1, and we want to calculate the probability of an event with temperature T -- that is, the change of occurence of temperature T.A few years ago Tamino calculated the probability spread using data for the continental US (USA48), and got the figure to the right. It's very close to a normal (Gaussian) distribution, and that's what I'll assume for the spread of probabilities. We're calculating the vertical distance between the blue and red curves, for any value of temperature along the x-axis.
As Wikipedia says,
So, if the background temperature is T1, the probability of the occurrence of a temperature T is
Now suppose the world gets warmer, and the background temperature changes from T1 to T2, both less than T. Let ΔT = T2 - T1 be the amount of warming.
There is a similar equation to the above for p(T,T2), the probability of an event with temperature T in the warmer world T2, just by replacing T1 above with T2. I'll assume the spread of the distributions, σ, is the same in both worlds.
We want to calculate the change in the probability, Δp, of the event with temperature T:
as a function of ΔT.
After some algebra, we find
where it's understood, just to make things look simplier, T, T1 and T2 are all divided by σ√2.
We can gnaw on this further to get
where I've used the fact that
(except maybe on Venus!). All the crap on the left-hand side is junk, not dependent on ΔT or T2. So we get
where f is some function we don't really care about here.
So -- for a temperature change ΔT, the probability of the occurrence of temperature T goes up exponentially with ΔT.
This, it seems to me, is proof of why extreme temperatures get much more likely in a warming world, faster than the linear amount by which the world warms.






13 comments:
David,
You are entirely missing the point. Let me explain in more detail. OF COURSE, as the earth warms you will get more extremes. That is obvious. But the larger the extreme (and we are in a very large one now), the smaller is the contribution of global warming induced by humans. In other words, without global warming we would STILL HAVE a heat wave and fires today.
The Northwest has warmed about 1 F over the past 80 years. Let's assume that is ALL due to human influence (it probably isn't, but lets assume so). Western WA has been 8-15F above normal the past week or so. Eastern WA 10-20F above normal. Take away the 1 F warming due to global warming. YOU STILL HAVE A MAJOR HEAT WAVE WITH VIRTUALLY THE SAME IMPACTS.
So the aphorism is quite correct...and I am not the only climate scientist saying this....for example, Martin Hoerling of NOAA ESRL has said the same thing.
..cliff
What nonsense from Cliff. If the probability of the heat wave was ~zero without warming then, to first order, all the of the impacts of the event are attributable to warming. (Without warming the event wouldn't have occurred so the impacts without warming are zero!)
To be more precise, you have to weight the impacts by the probabilities with and without warming, and the difference is the amount of impact attributable to warming.
In other words, without global warming we would STILL HAVE a heat wave and fires today.
I'm not sure we'd have a Ridiculously Resilient Ridge-induced heat wave though.
Best,
D
Cliff, you are assuming the climate system is linear, when it's not. Nonlinearities can easily add more energy to a regional subsystem.
For example, what effect has been the early melting snowpack this year, with its change in albedo. Less sunlight would have been reflected, and more absorbed.
"In other words, without global warming we would STILL HAVE a heat wave and fires today."
Maybe, but you don't know that. There simply are no model results of what the Northwest would be right now if AGW had never happened, starting in 1850 or whenever. Of course natural variability has a strong role in this. But it's absurd to say that AGW doens't because its effects are not linear.
I suggest you read these RealClimate posts, especially the quote from Hansen's 2012 PNAS paper:
http://www.realclimate.org/index.php/archives/2012/08/extreme-metrics/
http://www.realclimate.org/index.php/archives/2012/08/extreme-metrics/#ITEM-12692-0
"Take away the 1 F warming due to global warming. YOU STILL HAVE A MAJOR HEAT"VE WITH VIRTUALLY THE SAME IMPACTS."
It seems to me that even the premise of this argument is wrong. Why in the world would you compare the pdf of the global temperature to that of a particular land region such as the Western or Eastern part of the state of Washington?
Joe, I agree. For example, snowpack in the Cascades was very low this year and much of it melted early. That changes the albedo and means more heat is absorbed by the ground. That extra heat has consequences. I'm not saying it caused this heat wave, but it might have contributed more to this heat wave than just the AGW increase in background temperatures. Or other local considerations. It's just not correct to think of a heat wave, or any events now, as natural+AGW; they're complicated functions of natural and AGW, not simply their sum.
The internet needs more posts like this that attempt to explain the reasoning/justification behind the conclusions that scientists come to. Otherwise we're just the mysterious smart guys who somehow know everything.
Thanks for doing this.
It may be rather warm in the Pacific Northwest, but we are the exception. Through the first 5 days of July 2015 the USA48 as a whole is running cooler than the climate average by -0.4 degrees F. The mean temperature has been 72.8 while the climate average is 73.2:
http://www.atmos.washington.edu/marka/crn/201507.69.txt
How has the pdf changed in Salem where the temperature has been trending downward for the past 80 years:
http://www.atmos.washington.edu/marka/salem.1932_2013.png
The red line shows the downward trend in daily maximum temperature.
Cliff is very concerned about false positives, and this inclines him toward false negatives. In the extreme, Cliff argues like Johnny Cochran did in the OJ Simpson trial, "if the glove doesn't fit, you must acquit."
Doug: your comment was addressed to "Roy," and wasn't on the topic of this post. So I deleted it.
Mark Albright: Not sure if you're subscribed to these comments, but I looked at your graph giving the trend in annual daily maximum temperatures, which you showed as negative.
I agree. BUT the trend in annual daily average temperatures is positive:
http://davidappell.blogspot.com/2017/02/yes-salem-oregon-is-warming.html
Cliff: You waved your hands, but didn't supply any math, or why why my math is wrong.
Post a Comment